Updated : mar jun 6 20:01:42 CEST 2006
Grant propose la mise en oeuvre d'une grille de calcul à l'aide d'algorithmes biomimétiques. Cette grille de calcul étant conçue pour être mise en oeuvre sur de grands réseaux voir internet lui même doit avoir une forte robustesse et une bonne capacité d'adaptation. Les algorithmes biomimétiques sont de bons candidats pour répondre à ces besoins : ils sont conceptuellement adaptatifs et capables de fonctionner à partir d'informations incomplètes (erreurs de mesures, latances) ce qui est en pratique toujours le cas en situation réelle.
La grille est composée d'un ensemble de noeuds qui forment un réseau connexe. Chaque noeud ne permet d'atteindre qu'un nombre limité de noeuds voisins mais il doit exister au moins un chemin pour se rendre d'un noeud quelconque à un autre suivant cette relation de voisinage.
Chaque noeud peut soumettre des tâches à un autre qui lui pourra les relayer à un troisième, etc... Le problème fondamental de la répartition de charge devient assimilable à du routage. Une version biomimétique en est la collecte de nourriture par les fourmis : les noeuds sont des réservoirs plus ou moins importants de nourriture et les taches à faire éxecuter par les noeuds sont des fourmis.
L'ambition d'une grille déployable sur internet implique la capacité d'y accueillir des noeuds de toutes sortes : machines et systèmes d'exploitation variés. Ceci nous pousse à choisir des technologies portables pour le transport des requêtes et l'execution des tâches :
Le principal but de notre de grille et évidemment de réaliser les tâches confiées. Ces tâches sont des programmes tout à fait normaux dotés des points d'entrés necessaires à leur prise en charge par la grille. Par analogie avec les "servlet" et les "applets", nous avons baptisé de telles tâches "tasklets".
La première brique essentielle à la grille est le système de répartition de charge. Afin de proposer un service qui offre les même qualités de robustesse que l'internet lui-même il faut mettre en place un système capable de s'adapter aux aléas du réel et à l'incomplétude de sa connaissance. Le système de répartition de charge doit lui-même être réparti afin d'éviter les risque de saturation et de dysfonctionnement de l'ensemble de la grille qui serait du à ce seul point critique. La grille doit pouvoir résister autant que possible à la défaillance de quelques noeuds qui la constituent.
De plus la nature hétérogène de l'environnement ciblé ne permettra sans doute pas d'avoir une bonne connaissance à tout instant de l'état de chaque noeud :
Devant l'impossibilité pratique de collecter l'information nécessaire à une affectation idéale, un système adaptatif capable de faire des choix judicieux à partir d'observation incomplètes et/ou dégradées doit être en mesure d'affecter les tâches en vue d'optimiser l'utilisation des ressources disponibles.
Les algorithmes biomimétiques visent à simuler certains comportements du vivant pour en extraire la capacité d'adaptation à des situations changeantes et cela avec une perception parfois très limitée. Chaque être vivant doit résoudre quotidiennement des situations difficilement prévisible uniquement à l'aide d'information partielles. Le problème de la répartition de charge dans un contexte hétérogène et généraliste (i.e. les tâches à soumettre ne sont pas connues à l'avance donc il n'est pas possible de planifier leur réalisation).
La grille ne devant pas être commandée par un point central critique, nous nous interesserons plus particulièrement aux systèmes d'intelligences collectives. De tels systèmes sont composés de nombreux éléments très simples dont le comportement individuel ne présente aucun trait d'intelligence voire même un certaine bêtise. Mais lorsqu'ils sont déployés en nombres il émerge de leurs intéractions un comportement général qui paraît intelligent, ou tout du moins suffisament évolué pour résoudre des problème complexes [R1]. L'exemple le plus célèbre est la fourmilière : chaque fourmis a un comportement suffisament simple pour être assez facilement modélisé mais la colonie est capable de s'organiser pour affronter les aléas du monde dans lequelle elle est plongée.
Tous les noeuds de la grille sont donc d'un point de vue fonctionnel strictement identiques. Chacun est capable de prendre en charge le traitement d'une tâche ou de relayer une requête vers un autre noeud. Chaque noeud connaît un nombre limité de noeud voisin et la répartition de charge agit localement pour déterminer à quel noeud confier une requête : soi-même ou l'un des noeuds voisins connus. Evidemment le noeud choisi, voyant arriver la requête fait de même et éventuellement dirige lui-même la demande vers un troisième noeud, et ainsi de suite. Affecter une tâche à un noeud dans un tel réseau s'apparente à du routage, on parcourt le réseau noeud par noeud jusqu'à la destination avec la particulirité suivante : dans notre cas la destination n'est pas connue à priori.
Le modèle des fourmis à la recherche de nourriture a déjà été appliqué avec succès au routage adaptatif de paquets dans un réseau [R2]. Il est transposable à la répartition de charge dès que celle ci peut également être traitée comme un problème de routage. La non connaissance de la destination pour chaque requête ne pose pas de problème puisque le modèle utilisé répond au même critère en réalité : les sources de nourriture ne sont connues pas connues des fourmis. Elles sont découvertes au fur et à mesures et apparaissent ou disparaissent selon des événements non maîtrisés.
Le réseau de noeuds constitue l'environnement dans lequels les fourmis sont plongées. Les fourmis à la recherche de nourritures sont les taches à la recherche d'un processeur pour être éxécutées. Les fourmis parcours d'abord au hasard le réseau jusqu'à aboutir à un noeud qui les accepte. Lorsque le travail est terminé, le chemin ayant permis d'atteindre le noeud est marqué. Ce marquage plus ou moins éphémère servira ensuite aux autres fourmis à trouver un chemin menant à un processeur dans le réseau. Afin de répartir efficacement la tache, le marquage doit être proportionnel à la quantitié de nourriture, c'est à dire à la puissance de calcul disponible sur un noeud. Si un noeud devient trop chargé, les taches-fourmis en reviennent moins rapidement, le marquage vers ce noeud s'attenue et il apparaît alors comme un moins bon candidat.
Tout le problème de la répartition de charge se réduit maintenant à une gestion appropriée du marquage des liens inter-noeuds. Ce marquage peut être élémentaire. Un incrément fixe pour chaque terminaison de tâche est suffisant pour un renforcement des routes menant à de bons noeuds. Il est toutefois possible d'accélérer l'apprentissage du réseau en utilisant un marquage lié à la puissance constaté. Ainsi les incidences de situations trompeuses alétoires (par exemple tâche très courte affecté à un mauvais noeud) seront limitées. Le problème n'est pourtant pas trivial : il n'y a pas d'indice de puissance absolue : il est déjà difficile de classer des processeurs selon un axe de puissance unique. La mesure de la puissance réelle disponible peut s'appuyer sur un ou plusieurs de ces critère :
La fonction d'évaluation n'a toutefois pas besoin d'être totalement absolue sur tout le réseau, il suffit qu'il le soit pour tous les éléments pris en compte lors du routage d'une tâche. La fonction d'évaluation peut donc être locale à chaque noeud routeur si elle est appliquée de façon identique à tous les noeuds connus au niveau d'un noeud routeur.
De plus ces multiples critères d'évaluation permettent d'aller plus loin qu'une simple optimisation de l'affectation des noeuds. Il est aussi possible d'optimiser la topologie du réseau par la recherche des meilleurs chemins d'accès à la puissance de calcul.
Chaque noeud ne connais qu'un certain nombre d'autres noeuds auquel il est capable de relayer des requêtes. Cette relation de voisinage constitue une topologie qui selon ces caractéristiques aura une certaine influance sur les perforamances (robustesse, réactivité, ...) de la grille.
Dans cette première phase d'évaluation de l'algorithme de routage des taches, l'implémentation se réduit à un environnement hétérogène simulé sur un unique poste : ceci essentiellement pour des raisons économiques et pratiques. Le travail sera transposable directement à un véritable environnement réparti par une simple révision de l'implémentation des interfaces de communication entre noeud.
Le noeud de simulation est un noeud fonctionnel qui ajoute un délai au temps de traitement de la tache. Ce délai est fixe pour un noeud donnée mais varie d'un noeud à l'autre. Il simule la force de calcul plus ou moins importante d'un noeud par un retard artificiel de la fin de traitement d'une tache. Il s'ajoute un délai supplémentaire proportionnel à la charge du noeud, i.e. le nombre de tache en cours d'execution sur le noeud. Ce dernier point simule une baisse de performance en fonction du nombre de taches simultanément en execution.
Les taches soumises sont également un délai attribué aléatoirement afin de tester la répartition de taches hétérogène dont le temps de traitement n'est pas connu à priori. La performance globale de la grille sera simplement mesuré par l'écart entre le temps d'exécution réel de toutes les taches et la somme des délais de chaque tache qui représente le temps d'exécution optimal.
Le réseau testé contient 30 noeuds repartis sur une topologie arborescente : toutes les taches sont soumises à un premier noeud racine qui réparti sur une couche de 5 noeuds routeurs qui eux même répartissent chacun sur 6 noeuds de calcul.
Il y a trois types de noeuds : fort, moyen et faible, soit trois valeur de temporisation fixe possibles. Chaque branche finale ne contient que deux types de noeuds : soit faible/moyen, soit moyen/fort.
Notre répartitions de charge sera confronté à trois autres système à titre de comparaison :
Le système de séléction est évalué et confronté au système témoins (Random, RoundRobin, ...) dans un premier environnement simulé pour lequel le cout de charge est nul : les perofrmances de chaque noeud sont fixes et ne sont pas influancées par le nombre de taches en cours d'execution. Dans ce contexte la meiileure solution est de simplement affecter toutes les taches au même noeud, c'est à dire le meilleur disponible.
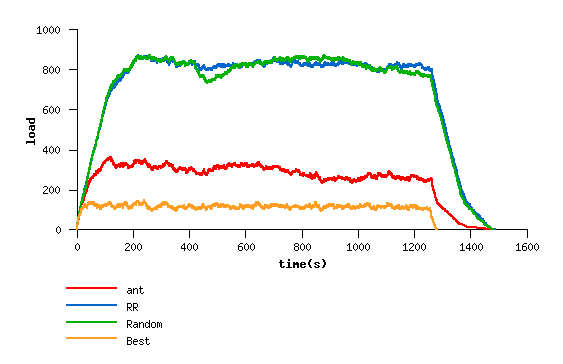
Grant, s'il parvient à approcher d'assez près le meilleur algorithme étalon, accuse un certain retard : des taches sont attribuées à de mauvais noeuds. Ces "mauvaises attributions" sont nécessaire et utilisée à des fin d'exploration.
En fait, si le cout de charge est nul, le mieux est simplement de ne pas répartir la charge du tout ! Ce que fait sans problème notre système étalon. Grant lui, tente de répartir la charge, la répartition ne se limite qu'à un sous-ensemble des meilleurs noeuds, mais des tâches ont du être envoyée sur chaque noeud avant que certains d'entre eux ne se démarquent significativement.
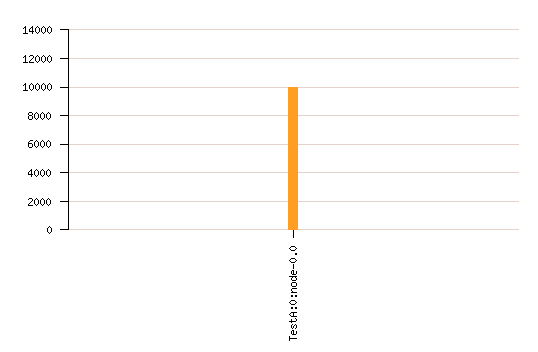
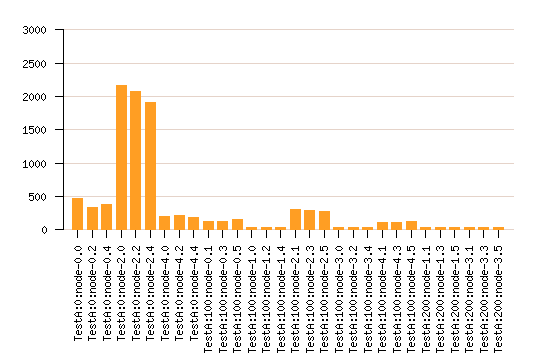
La répartition de charge RoundRobin est équivalente à une répartition purement aléatoire.
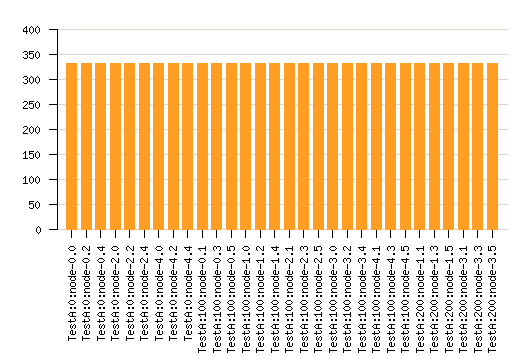
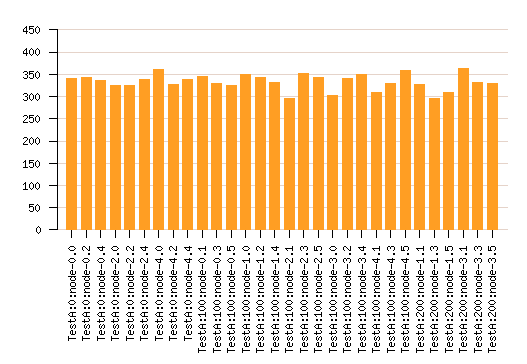
Dans un second temps, la capacité à s'adapter au variations de charge est testée en introduisant un coût de charge : chaque tache en cours d'execution sur un noeud, augmente le délai introduit pour simuler la consommation de ressources de calcul.
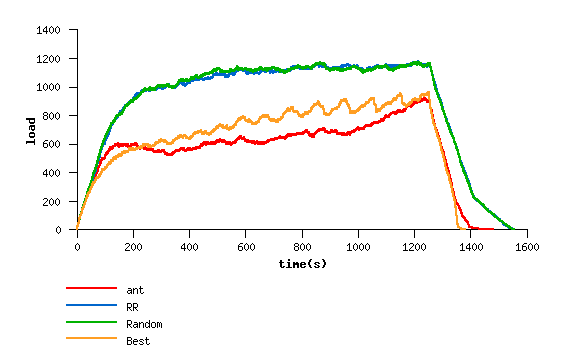
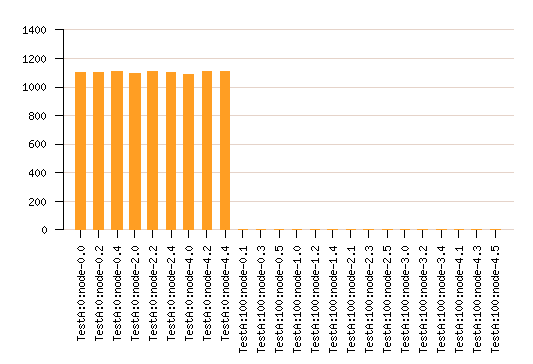
Si la répartition déterministe réparti bien la charge sur les meilleurs noeuds, elle ne parvient pas à la transferer suffisament sur les autres noeuds lorsque les meilleurs deviennent trop chargés.
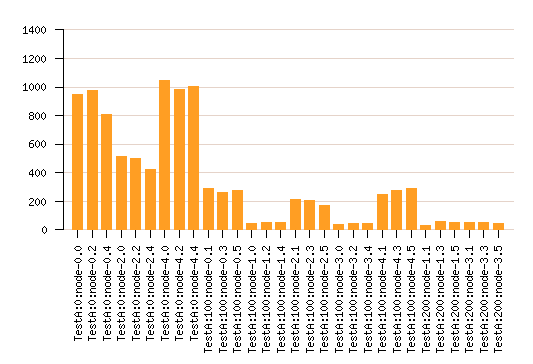
Ici grant parvient à mieux répartir la charge que notre algorithme étalon qui ne considère que les charges instantanées au moment de l'affectation. Son comportement exploratoire lui permet de mieux anticiper le report de charge sur les noeuds moins performants. L'algorithme utilisé pour étalonnage n'est pas en mesure d'anticiper quoi que ce soit. Seule la charge instantannée à l'instant de la soumission d'une tache est pris en compte alors qu'il faudrait idéalement considérer les charges futures à l'instant ou la tâche se terminera.
Copyright (C) 2004-2006 Sébastien DEVAUX